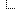Statistiques...
|
Statistiques...
|
Une question très simple : existe-t-il un tableau, quelque part, ou un petit programme indiquant la probabilité de remporter un assaut (dans un combat utilisant les règles de la série Défis fantastiques) en fonction de l'écart d'habileté entre les deux combattants ?
Jehan. 
14/08/2006, 14:31
L'excellent article d'Oiseau te dira tout ce que tu veux savoir à ce sujet, et même plus.
Justement non, il manque le cas où la différence est de -7.
 En fait, je demande ça parce qu'un détail du combat contre la Manticore, à la fin des Collines maléfiques, m'a toujours fait rire : le fait qu'un joueur-sorcier puisse envoyer des Gobelins au casse-pipe contre la bestiole. Pour rappel, les stats d'un Gobelin sont 5 et 5, celles Manticore sont 12 et 18... Je n'ai jamais cessé de me demander combien de Gob's il fallait massacrer pour venir à bout de la Manticore, alors je vais faire le calcul ici même, en espérant ne pas me gourer... (Oiseau, si tu me lis...) : Il y a 36 résultats possibles avec deux dés. À chaque assaut, chaque protagoniste lance les dés, il y a donc 36 * 36 combinaisons possibles, soit 1296 possibilités... Le Gobelin remporte l'assaut dans les cas suivants : Un score de 12 (1 chance sur 36) contre un score de 4 (3/36), 3 (2/36) ou 2 (1/36) : 7 cas sur 1296. Un score de 11 (2/36) contre un score de 3 (2/36) ou 2 (1/36) : 6 cas sur 1296. Un score de 10 (3/36) contre un score de 2 (1/36) : 3 cas sur 1296. Au total, le Gobelin possède 16 chances sur 1296 de remporter l'assaut, soit une probabilité de 0,012... L'assaut est nul dans les cas suivants : Un score de 12 (1/36) contre un score de 5 (4/36) : 4 cas sur 1296. Un score de 11 (2/36) contre un score de 4 (3/36) : 6 cas sur 1296. Un score de 10 (3/36) contre un score de 3 (2/36) : 6 cas sur 1296. Un score de 9 (4/36) contre un score de 2 (1/36) : 4 cas sur 1296. Par conséquent, les deux duellistes ont 20 chances sur 1296 de se neutraliser, soit une probabilité supérieure (un comble), de 0,016. La Manticore remporte donc l'assaut dans 1260 cas sur 1296, soit une probabilité de 0,972. Chaque Gobelin possède une endurance de 5, mais chaque coup ne lui en fait perdre que 2. Il faut donc trois assauts pour venir à bout d'un Gob'. Éliminons les cas nuls : le Gobelin a environ 2 % de chance de toucher la Manticore, qui elle fera mouche dans 98 % des cas. Autrement dit, il faut 50 assauts en moyenne au Gobelin pour toucher la Manticore, qui entre temps l'aura touché 49 fois. Sachant que la Manticore possède une endurance de 18, il lui faut neuf assauts pour mourir, ce qui arrivera donc au bout du 450ème assaut (ça fait long). Entre temps, les Gobelins auront mangé par 441 fois. On divise par trois : on obtient 147... Il faudra donc balancer 148 Gobelins à la Manticore pour qu'elle crève. CQFD. Si quelqu'un connaît l'anatomie des Gobelins en profondeur (les pervers, rasseyez-vous), et notamment le nombre de dents que possèdent ces créatures, il peut s'amuser à calculer le nombre de peaux-vertes que doit se farcir le héros avant d'aller défier la Manticore avec son armée. Easy, isn't it ? Ben oui mais non... Parce que ces calculs ne prennent pas en compte le cas où la Manticore fait usage de sa queue ! Pour la simple et bonne raison que je ne me souviens plus quel score le dé doit donner (5 ou 6, ou alors seulement 6 ?) pour que le coup porte, tuant le Gobelin instantanément. J'ajoute que ça complique beaucoup trop l'affaire pour moi. ^^ Il serait également intéressant de calculer combien de Gobelins devraient affronter la Manticore pour l'emporter en cas de combat simultané (la Manticore ne pouvant blesser qu'un Gobelin, mais pouvant être blessée par tous les autres). Mais on va mettre le principe de l'attaque un par un sur le fait qu'un Gobelin, c'est très con... Respect aux courageux qui sont arrivés jusqu'au bout de ce message vibraaant d'intérêt, et merci à Meneldur de m'avoir rappelé les stats de la Manticore, ainsi qu'à la calculatrice Windows... Jehan. 
14/08/2006, 18:02
Ah , ah!
Excellent , cette stat, j'adore! Tu n'a plus qu' a fire la meme avec OGR (geant hab:8 end:9)  Mais j'espere pour les gobs que la manticore sera morte de fatigue au 100eme... 
14/08/2006, 19:23
Il y a malheureusement une erreur dans ton raisonnement à la première étape :
Le Gobelin remporte l'assaut dans les cas suivants : Un score de 12 (1 chance sur 36) contre un score de 4 (3/36), 3 (2/36) ou 2 (1/36) : 7 cas sur 1296. Un score de 11 (2/36) contre un score de 3 (2/36) ou 2 (1/36) : 6 cas sur 1296. Un score de 10 (3/36) contre un score de 2 (1/36) : 3 cas sur 1296. Dans le cas d'un score de 12 (1 sur 36) contre un score de 4 ou 3 ou 2 (6 sur 36), les deux événements doivent se produire, et il faut alors multiplier les probabilités. On obtient ainsi 6/1296 et non 7/1296. Tu as multiplié les dénominateurs des fractions, mais additionné leurs numérateurs. Les deux autres cas sont correctement calculés, mais je pense que cela va changer légèrement le résultat final du problème. ^_^ 
14/08/2006, 19:27
Woow !
Même moi qui suis taré de chiffres et de stats, je ne me suis pas amusé à faire ce genre de calculs ! Il faut dire que mon penchant fourbe et cruel m'a fait sacrifier sans sourciller un ou deux Gobelins, pas plus, ça fait quand même perdre 1 point d'Endurance par Gobelin, (hé oui, aurais-tu oublié ce détail dans tes calculs, Jehan ?) histoire d'avoir le temps de préparer le sort suivant qui neutralise définitivement la Manticore. Ainsi, je ne dépense que 7 points d'Endurance en tout pour en venir à bout... et je m'épargne quelques maux de tête !! Mais pour la beauté de l'art, chapeau bas !
Aaargh... Merci Oiseau, même si cette légère erreur risque de ne pas m'arranger, j'étais si content de trouver 2 et 98 %, ça facilitait pas mal les calculs...
Bon, on recommence : Le Gobelin a donc 15 chances sur 1296 de blesser la Manticore. Soit une proba de 0,0116. La proba d'un assaut nul reste la même : 0,0154 La proba que la Manticore l'emporte est donc de 1261 chances sur 1296, soit 0,9730. Les trois probas additionnées donnent bien 1. On vire le résultat nul, et on obtient 0,0193 pour le Gobelin contre 0,9807 pour la Manticore. Bah au final, ça ne change pas grand chose, on peut arrondir à 2 et 98 %, je suis sûr que le résultat final sera le même à 1 Gobelin près. Mais comme je suis un fou furieux, j'ai réfléchi au problème de mort subite des Gobelins, due à la queue de la Manticore. Et j'ai trouvé comment l'intégrer au calcul ! De mémoire, à chaque assaut, la Manticore tue instantanément le Gob si le dé, lancé pour l'occasion, donne 5 ou 6. J'espère ne pas me tromper. Ce qui donne 1 chance sur 3 aux deux premiers assauts, le troisième étant de toute façon fatal au Gobelin. Ce qu'il faut comprendre, c'est que cette donnée supplémentaire ne change que la durée de vie moyenne d'un Gobelin, qui jusque-là était de trois assauts. Calculons donc la nouvelle espérance de vie de ces chères créatures... La probabilité qu'un Gobelin meurt au premier assaut est de 1/3. Jusque-là, ça va. La probabilité qu'un Gobelin meurt au second assaut est de 1/3, multipliée par la probabilité qu'il ne soit pas mort au premier assaut, qui elle est de 2/3. (C'est le principe de la loi géométrique, je crois bien.) Ce qui donne 2/9. La probabilité qu'un Gobelin meurt au troisième assaut est de 1, multipliée par la probabilité qu'il ne soit pas mort aux deux premiers assaut, qui est de 2/3 * 2/3, soit 4/9. 1/3 + 2/9 + 4/9 = 1, le compte est bon. Il ne reste plus qu'à faire une moyenne pondérée : 1/3 * 1 + 2/9 * 2 + 4/9 * 3 = 19/9 = 2,111111111111 (etc.). L'espérance de vie réelle d'un Gobelin est donc de 2,111111111111 assaut... Nous avons calculé plus haut qu'il fallait 450 assauts pour tuer la Manticore, dont 441 encaissés par les Gobelins. 441 / 2,111111111111 = (Tadaaa) 208,89 Il faudra donc 209 Gobelins pour abattre cette saleté de Manticore. À supposer, supposition hautement contestable, que chaque Gobelin ait 32 dents, le héros devra se farcir 7 Gobelins et posséder 210 points d'endurance pour abattre la Manticore avec sa petite armée... Je ne sais pas pourquoi, mais je crois que je vais rester sur MUR, FEU, HOR... Rappelons que les Gobelins sont cons et qu'ils attaquent un à un. Exercice : combien de Gobelins faudra-t-il dans le cas d'une attaque simultanée ? (Règle DF classique.) Jehan, qui remercie l'assistance. EDIT : Je me suis aperçu d'une grosse erreur dans le calcul de la moyenne, maintenant ça doit être bon. (Du moins je l'espère...)
15/08/2006, 01:48
Jehan a écrit :Exercice : combien de Gobelins faudra-t-il dans le cas d'une attaque simultanée ?Ha ! ha ! ha ! Celui qui calcule ça est fou. ^_^ 
15/08/2006, 12:35
Citation :le fait qu'un joueur-sorcier puisse envoyer des Gobelins au casse-pipe contre la bestiole. Non je ne parlerai pas de statistiques ici, ça me donne le tournis  C'est vrai que les auteurs de LDVELH ne sont pas toujours très copains avec les probas mais là il n'y a pas de problème. Le héros a toujours la possibilité de ne pas envoyer les gobelins et c'est au joueur de se rendre compte lui-même qu'envoyer les gobelins est inutile. 
Fléau des artificiers, les atogs, créatures légendaires, dévoraient des outils complexes afin de favoriser leur croissance bizarre.
15/08/2006, 15:21
Heu, il faut tenir compte aussi du fait que le joueur-sorcier n'a que 24 points d'Endurance au max. Donc il peut lancer 23 gobelins simultanément...
Finalement, la question est : combien faut-il de joueur-sorcier à 24 pointes d'Endurance. Et à ce rythme-là, une armée de joueurs sorciers auraient tôt fait de lancer un assaut contre le bastion de l'archimage.
Il ne faut pas attendre d'être heureux pour sourire... il faut sourire pour être heureux.
15/08/2006, 16:05
Oui, enfin c'était juste pour souligner le caractère un peu grotesque du sort GOB contre une Manticore que je me suis amusé à faire cette petite statistique. ^^
Jehan. 
17/05/2011, 14:43
je déterre cette antiquité vénérable pour souligner que la règle de base des combats contre plusieurs adversaires dans les DF est que les ennemis attaquent deux par deux; qu'ils soient trois ou soixante n'a pas d'importance, mis à part quelques créatures à l'agilité légendaire ils se mettent en colonne par deux et avancent bravement.
Il suffirait donc d'envoyer 105 gobelins au carnage. Ce qui, on en conviendra, change tout.
" Ashimbabbar m'a donné une dague et une épée et m'a dit
: Transperces-en ton corps; elles furent forgées pour toi." Poème d'Enheduanna 
19/05/2011, 07:16
Euh, tu es sûr de toi là? Je veux dire, pour le coup du "2 par 2" dans les combats des DF.
22/05/2011, 22:48
? C'est une des règles les plus basiques dans les DF…
" Ashimbabbar m'a donné une dague et une épée et m'a dit
: Transperces-en ton corps; elles furent forgées pour toi." Poème d'Enheduanna |
|
« Sujet précédent | Sujet suivant »
|
![[Image: vampire_icone.png]](http://traboule-segna.fr/PHP/img/vampire_icone.png)